1. Introduction
When establishing a statistical hypothesis to estimate a causal relationship, we allocate causes and effects as variables and establish a model. Hypothetically, researchers call the cause an independent variable and the result a dependent variable. In this article, the author explains the case when independent variables are discrete or categorical variables, i.e., patients are divided into two or more groups by the independent variable. Methods for testing whether a statistical difference exists in a dependent variable between the groups will be discussed. Mainly, the methods can be explained in two parts; 1) a continuous dependent variable and 2) a categorical dependent variable.
2. Comparison of a Continuous Dependent Variable between Groups
Researchers often analyze continuous dependent variables (i.e., weight, blood pressure, etc.) according to the independent variables that divide patients into groups (e.g., men vs. women, treatment drug A vs. treatment drug B vs. placebo, etc.). In this case, if the categorical independent variable separating the groups is X and the continuous dependent variable is Y, it is usually briefly expressed as the following:
Y~X
It is generally assumed that each group was sampled independently.
Statistical analysis methods to be used in continuous dependent variables are largely divided into parametric methods and nonparametric methods. The parametric methods can be used only when the dependent variable is normally distributed within each group. When using parametric methods, the mean is compared to the mean of another. Independent two-sample t-tests and ANOVA (analysis of variance) are the most widely known parametric methods.[1] Nonparametric methods can be used more generally, but are mostly used only when dependent variables are not normally distributed within at least one divided group.[2] Nonparametric methods compare distributions (not mean) such as rank to test differences of independent variables between groups. Nonparametric methods include the Wilcoxon rank-sum test and the Kruskal-Wallis test.[2]
3. Test of Normality and Equality of Variance
Within each group, the dependent variable must have a normal distribution to use parametric methods. For example, to compare the average weight of men vs. women, the weight of men AND the weight of women should have a normal distribution, respectively. However, there is no need for the weight of the total population to be normally distributed.
The test of normality can be seen through 1) the Shapiro-Wilk test and 2) the Kolmogorov-Smirnov test.[3] The general theory is that the Shapiro-Wilk test is suitable for small samples such as randomized controlled trials (RCT), and the Kolmogorov-Smirnov is suitable for representatives such as big data and large cohorts.[4] However, there is no strict distinction between the two of them. One should be careful when interpreting both tests because the null hypothesis is the distribution which satisfies normality. Therefore the case of P<0.05 should be interpreted as ‘not satisfying normality’. Additionally, the quantile-quantile (q-q) plot can be presented as evidence of normality. In the q-q plot, if the cases (expressed as points) are placed close to the q-q line, it can be said that the distribution is close to normal.
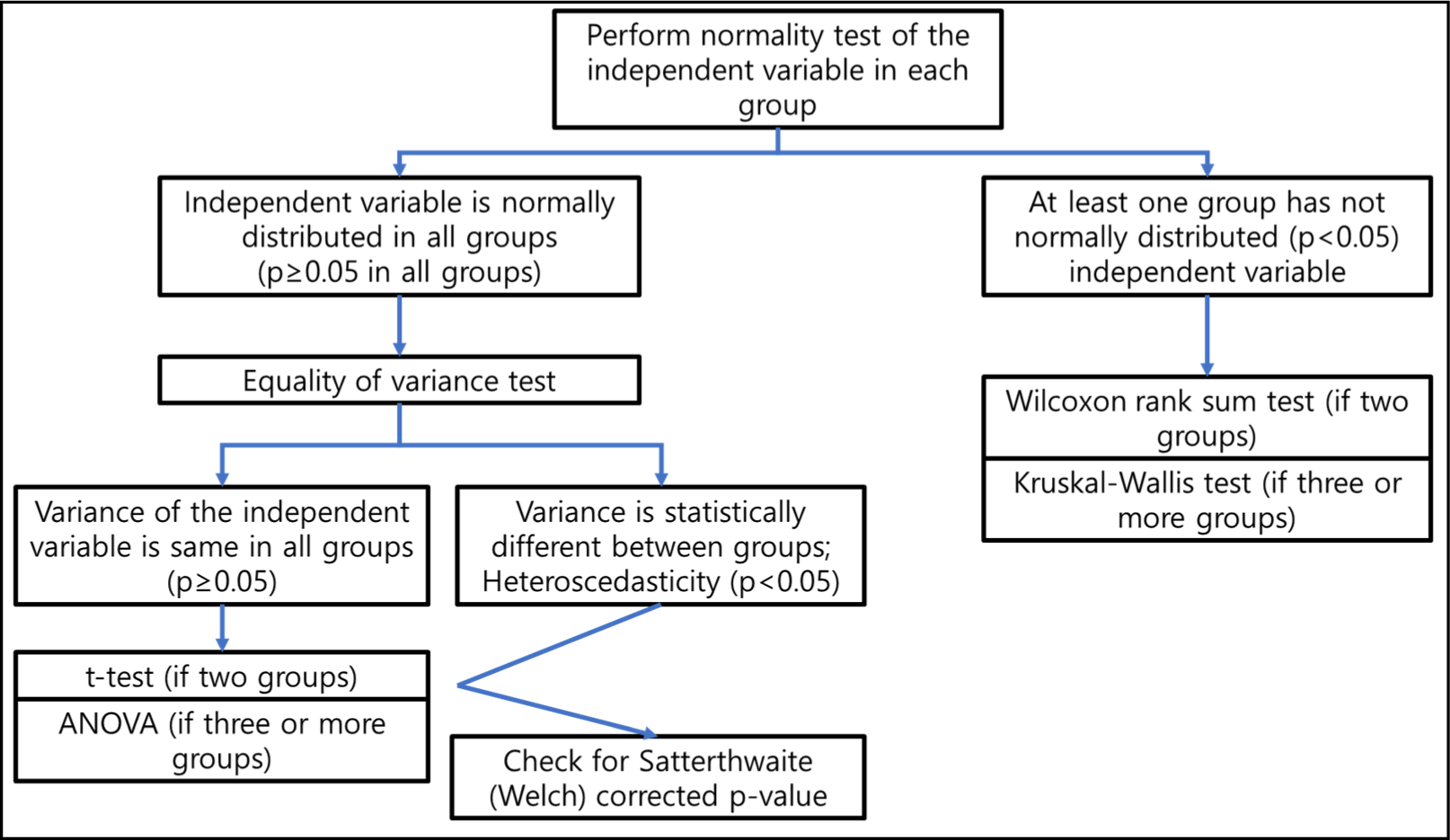
If the normality test satisfies the normality with P≥0.05, the equality of variance should be tested. The most famous methods are the Levene test, the Welch test, Bartlett test, and the (folded) F test. These methods are commonly used when there is no notable irregularity of distribution and there is no well-agreed criteria between the method selection. On the other hand, the Brown-Forsythe test is mainly used when the dependent variable has an irregular distribution.[5] The results of the equal variance tests should also be interpreted as ‘not satisfying the equal variance’ in the case of P<0.05, this case being called ‘heteroscedasticity’. Even when normality is satisfied but there is heteroscedasticity, t-test and ANOVA can be performed. When using these two tests in the case of heteroscedasticity, a P-value applied with a Satterthwaite (Welch) correction should be adopted. If the data has passed the normality assumption test, a t-test should be performed when there are two groups and an ANOVA test should be performed when there are three or more groups. If the normality assumption is not satisfied, the Wilcoxon rank-sum test is performed for two groups, and the Kruskal-Wallis test is performed for three or more groups. This method-choosing process is shown in Fig. 1.
4. Student’s t-test
The t-test is a test for defining the difference of the mean of the continuous variable between two groups.[6] In this case, ‘independent two-sample t-test’ is the full name of the test under the assumption of independence. Here, the alternative hypothesis (H1) implicates that the means of the dependent variable of the two groups are different, and the null hypothesis implicates that the means of the dependent variable of the two groups are equal. If the result of the test indicates that the P-value is less than 0.05, the alternative hypothesis is adopted. In this case, researchers describe it that “the dependent variable has statistical and significant differences between two groups.” This form of alternative hypothesis is called two-sided and is most commonly used. However, some researchers prefer a one-sided alternative hypothesis.
To explain the concept of a one-sided H1, it is assumeable that the group in which the average of the dependent variable is thought to be lower in the group 1. In this case, the one-sided alternative hypothesis is that the average of the dependent variables in Group 1 is lower than the average of the dependent variables in Group 2, and the null hypothesis is that the average of the dependent variable in the two groups are the same. This is used when it is almost certain that the mean of the dependent variable on one side is smaller and sometimes because of the advantage of decreasing the P-value, but generally not recommended. After this paragraph, the paper shall only deal with two-sided H1.
As a result of performing the t-test, if P<0.05, the difference between the two groups is statistically significant. For example, weight differs between sexes. However, if P≥0.05, there is no statistical difference. If t-test was used when normality assumption was satisfied but equality of variance assumption was not satisfied, Satterwaite (Welch) correction should be applied to the P-value, and in general, the P-value becomes slightly larger. If normality is not satisfied, convert the data to satisfy normality, or perform the Wilcoxon rank-sum test of the following section.[7]
5. Wilcoxon Rank-Sum Test
When comparing the two groups nonparametrically, the Wilcoxon rank-sum test, also known as the Mann-Whitney U test, is used.[8] At this stage, the null hypothesis indicates that the distributions of the dependent variable between the two groups are the same. The alternative hypothesis shows that the distributions of the dependent variable between the two groups are different. If P<0.05, it can be interpreted that there is a statistically significant difference in the distribution of dependent variables between the two groups. The example can be described that “the distribution of weight between genders differs significantly.” If P≥0.05, the situation can be explained that “there is no significant difference in weight distribution between genders”. Furthermore, if the overall shape of the distribution of the independent is similar in the two groups, the only difference will be the median. Therefore, in this case, “the distribution of weight between genders differs significantly” becomes “the median of weight between genders differs significantly”.
6. Analysis of Variance, ANOVA
When three or more groups are classified by independent variables, ANOVA is the most appropriate choice.[1] ANOVA is a parametric method, and therefore it is assumed that the dependent variable must follow a normal distribution within all groups of three or more but not necessarily in the whole observation. The null hypothesis is that the mean of all groups are the same, and the alternative hypothesis is that the mean of at least one group is different from that of another group. That is, if P<0.05, the means of all three groups is not equal.
Similarly, if the normal distribution is satisfied but the heteroscedasticity exists, looking into the P-value corrected by Satterthwaite (Welch) correction is recommended. The decisive difference between using a t-test multiple times and ANOVA is that the method can avoid repeating the statistical test. The conclusion of a single t-test is based on P<0.05, and 0.05 is the alpha value. In other words, it is possible to commit a type I error with a maximum chance of 5%. If there are five groups, a t-test must be performed 10 times for comparison between all groups, and the risk of committing a type I error increases by nearly 40%, as 0.9510 = 0.6 while ANOVA still has less than 5%.
7. Post-Hoc Analysis
If P<0.05 in ANOVA, then researchers might wonder which group is different from the others. The method for finding the difference among the groups after ANOVA is called the post-hoc analysis because it presupposes that ANOVA’s alternative hypothesis has been adopted in advance. The most famous post-hoc analyses for equal variance are Bonferroni and Tukey (called Tukey-Kramer).[9] These methods will show all combinations of P-values for each possible pair, e.g., 1-2, 1-3, and 2-3 for three groups. Here, in the case a pair marked as a P value<0.05, it can be interpreted that “there is a statistical difference of the means of the dependent variable between those two groups”.
Among two methods mentioned above, Tukey’s method is generally used when the number of observations is equal among each group, and Bonferroni’s method is used when the number of observations of each group is different. This is because the original Tukey (called Tukey’s Honest Significant Difference) before Kramer’s modification assumes that the sample sizes are equal.[10] In the case of unequal variance, the Games-Howell test is most widely used.[11] Table 1 summarizes the types of post-hoc analysis provided by SPSS 25.0 (IBM Corp., Armonk, NY, USA).[12-14]
8. Kruskal-Wallis Test
If the normal distribution assumption is not satisfied, the Kruskal-Wallis test can be used instead of ANOVA.[6] It distinguishes whether the distribution of variables of interest between three or more independent groups differs from each other. On such occasions, the null hypothesis is the equal distribution of dependent variables for all groups. The alternative hypothesis is that the distribution of the dependent variable of at least one group is different from another group. If all distributions are similar in shape, it can additionally be mentioned that the median differs between groups.
9. Nonparametric Post-Hoc Test
After the Kruskal-Wallis test, finding a simple, well-agreed post-hoc test method as in ANOVA is not easy. In general, nonparametric tests between two groups (i.e., Wilcoxon rank-sum test) are performed on all possible pairs, with an additional correction method applied to prevent increase of type I error as described previously. The results of this method, by a low change, may differ from the original Kruskal-Wallis test (i.e., the Kruskal-Wallis test shows that there is a difference between groups, but no difference between groups may be found in multiple corrected Wilcoxon rank-sum tests. Or vice versa). The most representative method of correction for multiple comparisons is Bonferroni, which divides the significance level (alpha) by the total number of comparisons. In other words, in the case of three groups, the criterion is strengthened to P<0.0166 (=0.05/3) instead of P<0.05. This is a very strict method, so it may be preferred for editors and reviewers, but in many cases, researchers do not prefer the Bonferroni. Alternatively, Holm (called Holm-Bonferroni), Hochberg, Homel, Benjamini-Hochberg, Šidák (called Dunn-Šidák), Benjamin-Yekutili can be used by researchers.[15]
10. Comparison of a Categorical Dependent Variable between Groups
The Chi-square (also chi-squared) test is used in situations where a categorical dependent variable (i.e., obesity vs. normal weight vs. underweight, high blood pressure vs. normal, etc.) is to be analyzed according to a categorical independent variable (i.e., male vs. female, drug A treatment group A vs. the placebo group, etc.).[16] The alternative hypothesis is that there is a correlation between the independent variable and the dependent variable, and the null hypothesis is that there is no correlation between the independent variable and the dependent variable. The null hypothesis is, in other words, that all groups are homogeneous. Therefore the chi-square test is sometimes referred to as the homogeneity test. When the result of the chi-square test indicates P<0.05, it can be explained that “there is a correlation between the independent variable and the dependent variable”.
During the process of the chi-square test, a table with cells is created by the number of categories of independent variables times the number of dependent variables. It is re-commended that researchers look into this table carefully, and if there is at least one cell that has a frequency of five or less, an additional correction is required for the P-value. The correcting process is called the Fisher exact test. The interpretation method of the P-values of the Fisher exact test is the same as the chi-square test.[16]
11. Special Cases of Categorical Dependent Variables
In some cases, the categorical variable of concern acts as a continuous variable. For example, months (January to December), drug dosage (low dose, medium dose, high dose), physical activity (insufficient activity, intermediate activity, high activity) are such cases.[17, 18] On these occasions, the Cochran-Armitage trend test may be used instead of the chi-square test.
In other cases, the dependent variable and the independent variable are not independently sampled. For example, when researchers check the effect of a specific treatment, they set the dependent variable as symptom existence before treatment and set the independent variable as symptom existence before treatment of the same patients. In this case, the assumption of independent sampling is violated, and therefore the McNemar test (or Cochran’s Q test) instead of the chi-square test should be applied.
12. Post-Hoc Analysis for Chi-Square Test
The chi-square test is used in the same way even when the independent variable divides patients into three or more groups. This is in contrast to the case of continuous dependent variables which had to use ANOVA instead of t-test if the number of groups was three or more. However, it could be preferable to know which groups made statistical significance if the test result is P<0.05 when there are more than three groups. In this case, similar to the nonparametric post-hoc test, the chi-square tests between all group pairs should be performed, with the correction method mentioned above applied, such as Bonferroni.[19]
13. Conclusion
Statistical analysis for categorical independent variables is the most common situation in medical and related statistical studies. Recent medical journals tend to hire separate statistical reviewers, and if a paper is submitted without paying enough attention to the statistical method, the author may face strong criticism due to it. Therefore, it is always encouraged to understand the statistical methods of this article so that one can reduce statistical criticism and publish statistically robust research.







